Introduction and Project Seeds
CSE 662 Fall 2019
August 27
Logistics

Oliver Kennedy
Capen 212
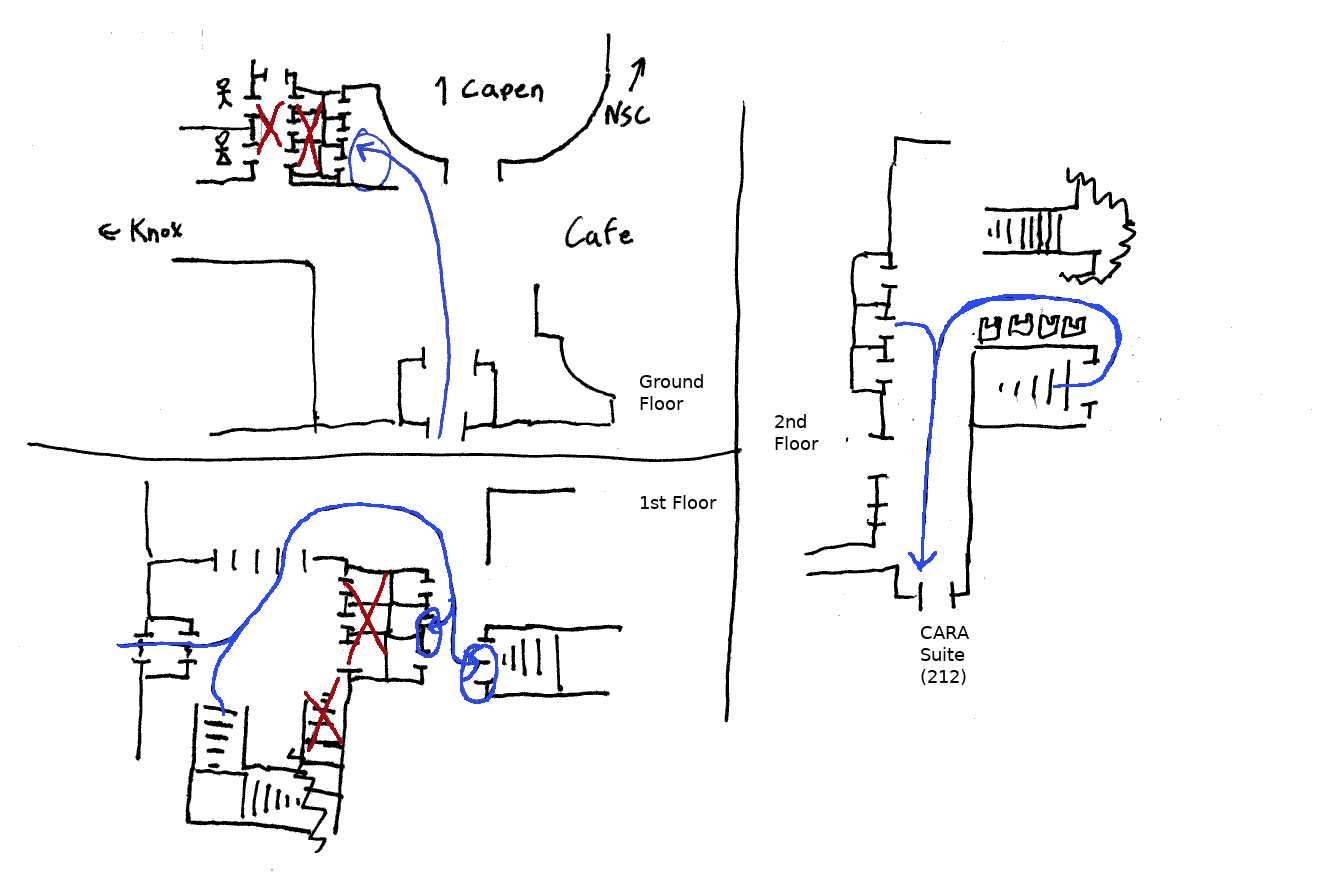
- Course Website
https://odin.cse.buffalo.edu/teaching/cse-662 - Grading
- Group Project: 3 Reports (15%, 15%, 50%)
- Weekly Papers and In-Class Discussion (20%)
- Office Hours
- Oliver: Weds 3:30 PM-4:50 PM (Before Class)
Always add [CSE662] to the title of emails
- This helps me to reply to your email faster
- The tag is for assignments
Academic Integrity
Each group will have a separate project. I don't expect cheating to be an issue, but to be clear...
- I encourage you to talk to your classmates about ideas and papers out of class.
- I expect you to work with your team on the project.
- You should use outside tools/code/libraries (with attribution) if they're useful.
- If you/your team submits something as your work... it had better be your work.
DB ≈ PL
| Databases | Programming Languages |
|---|---|
| Indexes | Data Structures |
| Transactions/Logging | Software Transactional Memory |
| Incremental Views | Self-Adapting Computation |
| Query Rewriting / Performance Models | Compiler Optimization / Program Analysis |
| Probabilistic DBs | Probabilistic Programming |
DB ≈ PL
Course Structure
- Data Structures, Indexes, Adaptive Indexing
- Uncertainty in Data
- High-Throughput Data Processing
- Combining DB+PL for Machine Learning
Course Structure
| Tuesday | Thursday |
|---|---|
| Classical Lecture (Paper of the Week) |
Group Presentations and Meetings |
Paper Discussion
- One paper every week (Assigned by Thursday Night).
- I will be calling on random people to answer questions about the paper.
- Every group will be asked to present one paper pertinent to your project.
- Class participation is 20% of your grade.
Group Presentations
- Present background, work-in-progress, your design choices, algorithms, information, code, performance metrics and/or analysis.
- Defend your ideas and design choices in a public setting.
- Everyone must attend.
- I will be calling on random people to ask questions of the presenters.
- Class participation is 20% of your grade.
Class Participation
I use a 3 point system:
- 0 points: You're not here when I call on you
- 2 points: You have a meaningful comment/question about the project/paper
- 1 points: Everything else
You get 2 excused absences (guarantees I won't call on you) for the term. You must let me know beforehand
Project Submissions
Checkpoint 1: Project Description (Due Sept 25, 11:59)
- What is the specific challenge that you will solve?
- What metrics will you use to evaluate success?
- What deliverables will you produce?
Project Submissions
Checkpoint 2: Progress Report (Due Oct 23, 11:59)
- What challenges have you overcome so far?
- How does your existing work compare to other, similar approaches?
- What design decisions have you made so far and why?
- How have your goals changed from checkpoint 1?
- What challenges remain for you to overcome?
Project Submissions
Checkpoint 3: Final Report (Due Dec 6, 11:59)
- What specific challenges did you solve?
- How does your final solution compare to other, similar approaches?
- Were the design decisions you made correct and why?
Paper Assignment 1
Lazy evaluation of transactions in database systems
Jose M. Faleiro, Alexander Thomson, Daniel J. Abadi
Be ready to intelligently discuss the paper's contents Tuesday Sept. 3
Class Introductions
- What is your name?
- What did you do over the summer?
- Why did you take this class?
- What is the most recent nonfiction TV/Movie/Book you've read/etc...?
Project Seeds
- Replicate Learned Data Structures
- Replicate CrimsonDB
- Linear Algebra Optimizer for Spark
- Simulating Data from SQL Logs
- Reenactment-style Updates
- Schema Discovery for Data Directories
Replicate Learned Data Structures
CDF-Based Indexing
"The Case for Learned Index Structures"
by Kraska, Beutel, Chi, Dean, Polyzotis
Cumulative Distribution Function (CDF)
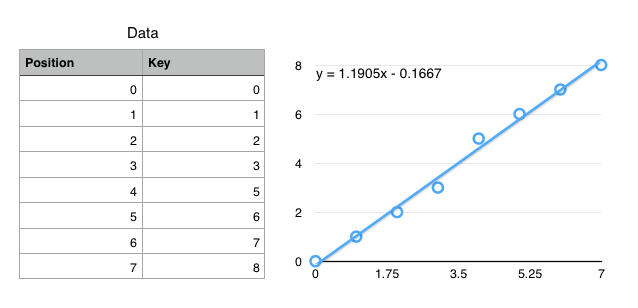
$f(key) \mapsto position$
(not exactly true, but close enough for today)
Using CDFs to find records
- Ideal: $f(k) = position$
- $f$ encodes the exact location of a record
- Ok: $f(k) \approx position$
$\left|f(k) - position\right| < \epsilon$ - $f$ gets you to within $\epsilon$ of the key
- Only need local search on one (or so) leaf pages.
Simplified Use Case: Static data with "infinite" prep time.
How to define $f$?
- Linear ($f(k) = a\cdot k + b$)
- Polynomial ($f(k) = a\cdot k + b \cdot k^2 + \ldots$)
- Neural Network ($f(k) = $
 )
)
We have infinite prep time, so fit a (tiny) neural network to the CDF.
Neural Networks
- Extremely Generalized Regression
- Essentially a really really really complex, fittable function with a lot of parameters.
- Captures Nonlinearities
- Most regressions can't handle discontinuous functions, which many key spaces have.
- No Branching
ifstatements are really expensive on modern processors.- (Compare to B+Trees with $\log_2 N$ if statements)
The community is skeptical!
Try to repeat the author's success!
Try to find overlooked problems with the author's success!
Things to think about
- How did they achieve their performance gains. Is it what they're claiming, or a side-effect?
- Are their performance gains workload specific? Are there workloads on which those gains go away?
- Are there notable design considerations that were not documented?
Replicate CrimsonDB
When disks are involved, sorted data layouts are fantastic for reads! $O(1)$ IOs to access any data.
... but horrible for writes. $O(N)$ IOs for writes. ($O(N^2)$ total cost)
Idea 1: Add a buffer. Now each buffer merge is $O(N)$ IOs. ($O(\frac{N^2}{B}$ total cost)
Idea 2: Multiple layers of buffers. Merge buffers with other siilarly sized buffers. ($O(N\log(N))$ total cost)
Log Structured Merge Trees
- Dozens of variants which each adjust slightly different knobs
- CrimsonDB:
- Catalog existing knobs
- Develop a unified infrastructure for adjusting all the knobs
- Figure out which knobs are right for a given workload
Things to think about
- How did they achieve their performance gains. Is it what they're claiming, or a side-effect?
- Are their performance gains workload specific? Are there workloads on which those gains go away?
- Are there notable design considerations that were not documented?
Linear Algebra Optimizer for Spark

Types
- Matrix
- Vector
- Scalar
Operations
- Multiply
- Add
- ...
Everything reduces to a small set of primitive operations with well-defined equivalence rules and simplifications.
Idea: Write an optimizer!
One approach Scalable Linear Algebra on a Relational Database System
Leverage an existing relational database optimizer to schedule execution for evaluating a linear algebra expression
Another approach Spark MLLib Linear Methods
Unoptimized implementation directly over Spark RDDs (Top Hit: "Spark for Linear Algebra: don't - ChapterZero")
Apples-to-apples comparison
Ideas: Combine the Two: Linear algebra over Spark DataFrames/Catalyst, and/or build your own optimizer
Things to think about
- How do you represent matrices / vectors in Spark?
- How do you map Linear Algebra operations onto SQL/DataFrame operations?
- Are optimizations specific to Linear Algebra that you can take advantage of?
Simulating Data from SQL Logs
How do you benchmark database systems?
Idea 1
Find a dataset
What (representative) queries do you ask?
Idea 2
Find a query log
Data is often full of PIID and harder to access
Easy to get data OR queries, but hard to get both.
Idea 3: Get one from the other.
SQL Logs
- UPDATE / INSERT / DELETE
- Explicitly given records in the dataset
- SELECT
- Constraints on the data in the dataset
SELECTs as constraints
- SELECT A, B, ... FROM R, S
- A, B, ... are columns in either R or S
- WHERE A = 5
- 5 is a value in column A
- GROUP BY B
- B is categorical
You may also have affected-row counts
Given a log of SQL queries + DDL expressions, generate a (representative) dataset that the query log will run over.
Example: Phone Lab Trace
Example: Sloan Digital Skyserver
Things to think about
- What kind of constraints can you extract from the log?
- How do you go from a set of constraints to a data distribution?
- Does your scheme work for SDSS?
- What makes a dataset "representative"?
Reenactment-style Updates
- Dataset Versioning
- UPDATE/DELETE/INSERT are not reversible; Creating entire copies of a datset is slow/wasteful, and may be much larger than the update.
- Provenance
- Tons of work to understand data dependencies in SQL queries. Less so on updates.
- Slow Updates
- Committing updates is slow. Can't answer queries until data committed.
Reenactment
UPDATE foo SET A = 1 WHERE B > 5;
Replace DDL/DML operations with equivalent "reenactment queries"
CREATE VIEW foo_v2
SELECT CASE WHEN B > 5 THEN 1 ELSE A END AS A
B, C, D, ...
FROM foo_v1;
- Dataset Versioning
- Each version can be recovered by re-executing queries
- Provenance
- Every version is a query.
- Slow Updates
- Adding another query to the stack is fast.
But you wind up with gnarly queries...
- Reenactment-specific query optimizer.
- Periodic version materialization
- Encoding DDL/DML in special tables.
Things to think about
- How do you store the update history?
- Can you answer queries directly from the update history?
- Try out different things, you might be surprised how things break.
Learning Data Directory Schemas
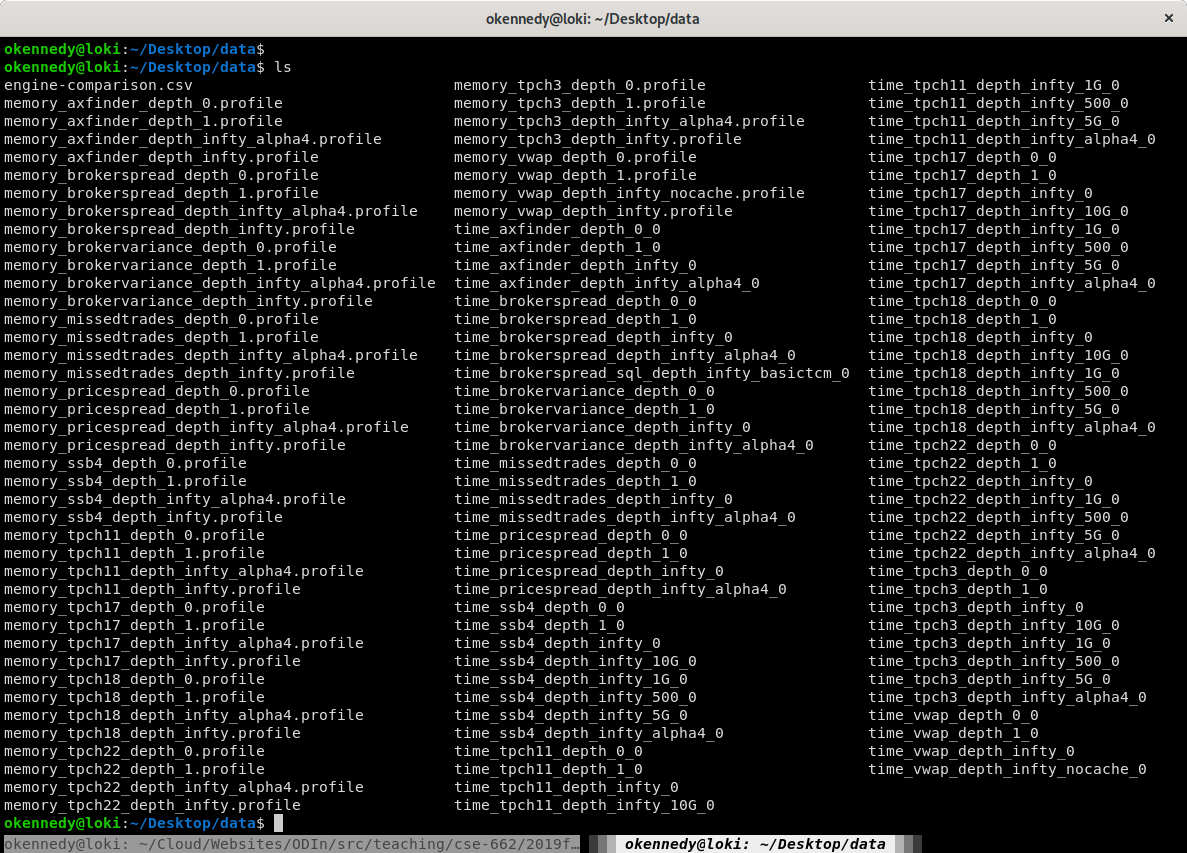
Experimental Data
- One file per trace
- File formats unknown
- Directory structure "sort of" organized
- File naming is "sort of" consistent
I want a graph!
- Reverse engineer the directory structure.
- Figure out the right pattern to get the right files.
- Figure out and handle outliers.
- Parse the files into one or more data tables.
- ... then start thinking about graphing
Idea: Automate table extraction
Directory → Table[s]
Tables
- One table per file
- Not much better than the directory
- One big table
- May be multiple entity types in the data
Things to think about
- What types of file schemas can you support?
- How do you decide that two files are of the same entity?
- Can you detect semantic information in the filenames? (e.g., phrase correlated with entity)
- Filenames may combine multiple semantic elements
(Project co-advised by William Spoth)