Today's Focus

$\sigma_C(R)$ and $(\ldots \bowtie_C R)$

(Finding records in a table really fast)

$\sigma_{R.A = 7}(R)$

Where is the data for key 7?

Option 1: Linear search

$O(N)$ IOs

Initial Assumptions

Data is sorted on an attribute of interest (R.A)

Updates are not relevant

$O(\log_2 N)$ IOs

Better, but still not ideal.

Idea: Precompute several layers of the decision tree and store them together.

Fence Pointers

... but what if we need more than one page?

Add more indirection!

ISAM Trees

Worst-Case Tree?

Best-Case Tree?

It's important that the trees be balanced

... but what if we need to update the tree?

Challenges

• Finding space for new records
• Keeping the tree balanced as new records are added

Idea 1: Reserve space for new records

Just maintaining open space won't work forever...

Rules of B+Trees

Keep space open for insertions in inner/data nodes.

‘Split’ nodes when they’re full

Avoid under-using space

‘Merge’ nodes when they’re under-filled

Maintain Invariant: All Nodes ≥ 50% Full

(Exception: The Root)

Deletions reverse this process (at 50% fill).

$\sigma_C(R)$ and $(\ldots \bowtie_C R)$

Original Query: $\pi_A\left(\sigma_{B = 1 \wedge C < 3}(R)\right)$

Possible Implementations:

$\pi_A\left(\sigma_{B = 1 \wedge C < 3}(R)\right)$

Always works... but slow

$\pi_A\left(\sigma_{B = 1}( IndexScan(R,\;C < 3) ) \right)$

Requires a non-hash index on $C$

$\pi_A\left(\sigma_{C < 3}( IndexScan(R,\;B=1) ) \right)$

Requires a any index on $B$

$\pi_A\left( IndexScan(R,\;B = 1, C < 3) \right)$

Requires any index on $(B, C)$

Lexical Sort (Non-Hash Only)

Sort data on $(A, B, C, \ldots)$

First sort on $A$, $B$ is a tiebreaker for $A$,
$C$ is a tiebreaker for $B$, etc...

All of the $A$ values are adjacent.

Supports $\sigma_{A = a}$ or $\sigma_{A \geq b}$

For a specific $A$, all of the $B$ values are adjacent

Supports $\sigma_{A = a \wedge B = b}$ or $\sigma_{A = a \wedge B \geq b}$

For a specific $(A,B)$, all of the $C$ values are adjacent

Supports $\sigma_{A = a \wedge B = b \wedge C = c}$ or $\sigma_{A = a \wedge B = b \wedge C \geq c}$

...

For a query $\sigma_{c_1 \wedge \ldots \wedge c_N}(R)$

1. For every $c_i \equiv (A = a)$: Do you have any index on $A$?
2. For every $c_i \in \{\; (A \geq a), (A > a), (A \leq a), (A < a)\;\}$: Do you have a tree index on $A$?
3. For every $c_i, c_j$, do you have an appropriate index?
4. A simple table scan is also an option

Which one do we pick?

(You need to know the cost of each plan)

These are called "Access Paths"

Strategies for Implementing $(\ldots \bowtie_{c} S)$

Sort/Merge Join

Sort all of the data upfront, then scan over both sides.

In-Memory Index Join (1-pass Hash; Hash Join)

Build an in-memory index on one table, scan the other.

Partition Join (2-pass Hash; External Hash Join)

Partition both sides so that tuples don't join across partitions.

Index Nested Loop Join

Use an existing index instead of building one.

Index Nested Loop Join

1. Read one row of $R$
2. Get the value of $a = R.A$
3. Start index scan on $S.B > a$
4. Return all rows from the index scan
5. Read the next row of $R$ and repeat

Index Nested Loop Join

1. Read one row of $R$
2. Get the value of $a = R.A$
3. Start index scan on $S.B\;[\theta]\;a$
4. Return all rows from the index scan
5. Read the next row of $R$ and repeat

Data Organization

Data Organization

Data Organization

Unordered Heap

$O(N)$ reads.

Sorted List

$O(\log_2 N)$ random reads for some queries.

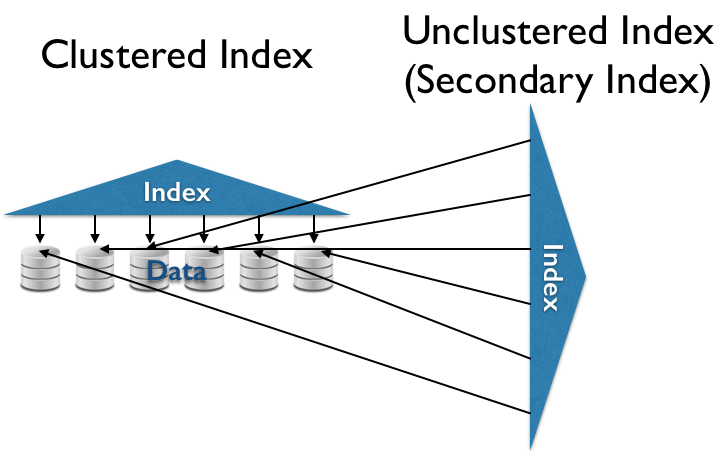
Clustered (Primary) Index

$O(\ll N)$ sequential reads for some queries.

(Secondary) Index

$O(\ll N)$ random reads for some queries.

Problems

$N$ is too small

Too many overflow pages (slower reads).

$N$ is too big

Too many normal pages (wasted space).

To keep things simple, let's use $$h(k) = k$$

(you wouldn't actually do this in practice)

Changing hash functions reallocates everything randomly

Need to keep the entire source and hash table in memory!

if $h(k) = x \mod N$

then

$h(k) =$ either $x$ or $2x \mod 2N$

Each key is moved (or not) to precisely one of two buckets in the resized hash table.

Never need more than 3 pages in memory at once.

Changing sizes still requires reading everything!

Idea: Only redistribute buckets that are too big

Add a directory (a level of indirection)

• $N$ hash buckets = $N$ directory entries
  (but $\leq N$ actual pages)
• Directory entries point to actual pages on disk.
• Multiple directory entries can point to the same page.
• When a page fills up, it (and its directory entries) split.

Dynamic Hashing

• Add a level of indirection (Directory).
• A data page $i$ can store data with $h(k)%2^n=i$ for any $n$.
• Double the size of the directory (almost free) by duplicating existing entries.
• When bucket $i$ fills up, split on the next power of 2.
• Can also merge buckets/halve the directory size.