Querying Incomplete Databases
CSE-4/562 Spring 2019
May 1, 2019
Textbook: PDB Concepts and C-Tables

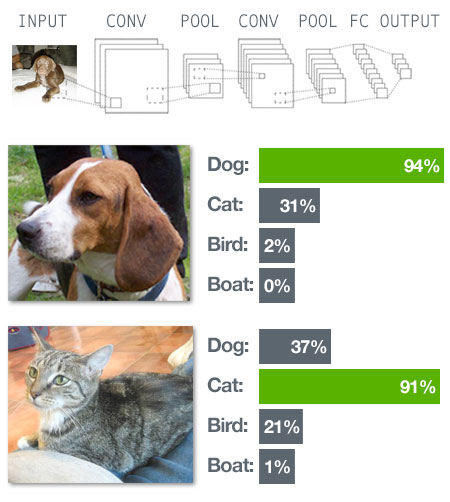
What happens when you don't know your data precisely?
SELECT * FROM Posts WHERE image_class = 'Cat';
SELECT COUNT(*) FROM Posts WHERE image_class = 'Cat';
SELECT user_id FROM Posts
WHERE image_class = 'Cat'
GROUP BY user_id HAVING COUNT(*) > 10;
Incomplete Databases
↓
Probabilistic Databases
- Representing Incompleteness
- Querying Incomplete Data
- Implementing It
| or |
|
Incomplete Database ($\mathcal D$): A set of possible worlds
Possible World ($D \in \mathcal D$): One (of many) database instances
(Require all possible worlds to have the same schema)
What does it mean to run a query on an incomplete database?
$Q(\mathcal D) = ?$
$Q(\mathcal D) = \{\;Q(D)\;|\;D \in \mathcal D \}$
| or |
|
$$Q_1 = \pi_{Name}\big( \sigma_{state = \texttt{'NY'}} (R \bowtie_{zip} ZipLookups) \big)$$
| { |
| or |
|
} |
| or |
|
$$Q_2 = \pi_{Name}\big( \sigma_{region = \texttt{'Northeast'}} (R \bowtie_{zip} ZipLookups) \big)$$
| { |
| or |
|
} |
| or |
|
$$Q_2 = \pi_{Name}\big( \sigma_{region = \texttt{'Northeast'}} (R \bowtie_{zip} ZipLookups) \big)$$
| { |
|
} |
Challenge: There can be lots of possible worlds.
Observation: Possibilities for database creation break down into lots of independent choices.
Factorize the database.
|
| ||||||||||||||||||||||||
|
|
Alice appears in both databases.
The only differences are Bob and Carol's zip codes.
List Out Choices
- $\texttt{bob}$$ \in \{ 4, 9 \}$ (Bob's zip code digit)
- $\texttt{carol}$$ \in \{ 3, 8 \}$ (Carol's zip code digit)
| $\mathcal R$ | Name | ZipCode |
|---|---|---|
| 1 | Alice | 10003 |
| 2 | Bob | 14260 |
| 3 | Bob | 19260 |
| 4 | Carol | 13201 |
| 5 | Carol | 18201 |
$\big[\;\texttt{bob} \in \{4, 9\},\; \texttt{carol} \in \{3, 8\}\;\big]$
| $\mathcal R$ | Name | ZipCode | |
|---|---|---|---|
| 1 | Alice | 10003 | → always |
| 2 | Bob | 14260 | → if $\texttt{bob} = 4$ |
| 3 | Bob | 19260 | → if $\texttt{bob} = 9$ |
| 4 | Carol | 13201 | → if $\texttt{carol} = 3$ |
| 5 | Carol | 18201 | → if $\texttt{carol} = 8$ |
$\big[\;\texttt{bob} \in \{4, 9\},\; \texttt{carol} \in \{3, 8\}\;\big]$
| $\mathcal R$ | Name | ZipCode | |
|---|---|---|---|
| 1 | Alice | 10003 | → a |
| 2 | Bob | 14260 | → b |
| 3 | Bob | 19260 | → c |
| 4 | Carol | 13201 | → d |
| 5 | Carol | 18201 | → e |
Pick one of each: $\big[\;\{a\},\; \{b, c\},\; \{d, e\}\;\big]$
Set those variables to $T$ and all others to $F$
$R_1 \equiv \big[a \rightarrow T, b \rightarrow T, d \rightarrow T, * \rightarrow F\big]$
| $\mathcal R$ | Name | ZipCode | |
|---|---|---|---|
| 1 | Alice | 10003 | → T (a) |
| 2 | Bob | 14260 | → T (b) |
| 3 | Bob | 19260 | → F (c) |
| 4 | Carol | 13201 | → T (d) |
| 5 | Carol | 18201 | → F (e) |
Use provenance as before...
... but what about aggregates?
SELECT COUNT(*)
FROM R NATURAL JOIN ZipCodeLookup
WHERE State = 'NY'
$$= \begin{cases} 1 & \textbf{if } \texttt{bob} = 9 \wedge \texttt{carol} = 8\\ 2 & \textbf{if } \texttt{bob} = 4 \wedge \texttt{carol} = 8 \\&\; \vee\; \texttt{bob} = 9 \wedge \texttt{carol} = 3\\ 3 & \textbf{if } \texttt{bob} = 4 \wedge \texttt{carol} = 3 \end{cases}$$
Problem: A combinatorial explosion of possibilities
Idea: Simplify the problem
- Is a particular tuple Possible?
- Is a particular tuple Certain?
- Certain Tuple
- A tuple that appears in all possible worlds
- $\forall D \in \mathcal D : t \in D$
- Possible Tuple
- A tuple that appears in at least one possible world
- $\exists D \in \mathcal D : t \in D$
Non-aggregate queries
- Is a tuple Certain?
- Is the provenance polynomial a tautology?
- Is a tuple Possible?
- Is the provenance polynomial a contradiction?
Pick your favorite SAT solver, plug in and go
Aggregate queries
As before, factorize the possible outcomes
$$1 + \{\;1\;\textbf{if}\;\texttt{bob} = 4\;\} + \{\;1\;\textbf{if}\;\texttt{carol} = 3\;\}$$
Not bigger than the aggregate input...
...but at least it only reduces to bin-packing
(or a similarly known NP problem.)