Midterm Review
CSE-250 Fall 2022 - Section B
Oct 17, 2022
Scala
Scala Types
| Type | Description | Examples |
|---|---|---|
| Boolean | Binary value | true, false |
| Char | 16-bit unsigned integer | ‘x’, ‘y’ |
| Byte | 8-bit signed integer | 42.toByte |
| Short | 16-bit signed integer | 42.toShort |
| Int | 32-bit signed integer | 42 |
| Long | 64-bit signed integer | 42l |
| Float | Single-precision floating-point number | 42.0f |
| Double | Double-precision floating-point number | 42.0 |
| Unit | No value | () |
Scala Types
Mutable vs Immutable
- Mutable
- Something that can be changed
- Immutable
- Something that can not be changed
- val: A value that can not be reassigned (immutable)
- var: A variable that can be reassigned (mutable)
Mutable vs Immutable
scala> val s = mutable.Set(1, 2, 3)
scala> s += 4
scala> println(s.mkString(", ")
1, 2, 3, 4
If a val points to a mutable object, the mutable object can still be changed.
Logarithms
Logarithms
- Let $a, b, c, n > 0$
- Exponent Rule: $\log(n^a) = a \log(n)$
- Product Rule: $\log(an) = \log(a) + \log(n)$
- Division Rule: $\log\left(\frac{n}{a}\right) = \log(n) - \log(a)$
- Change of Base from $b$ to $c$: $\log_b(n) = \frac{\log_c(n)}{\log_c(b)}$
- Log/Exponent are Inverses: $b^{\log_b(n)} = \log_b(b^n) = n$
Growth Functions
Growth Functions
Assumptions about $f(n)$
- Problem sizes are non-negative integers
- $n \in \mathbb Z^+ \cup \{0\}$
- We can't reverse time
- $f(n) \geq 0$
- Smaller problems aren't harder than bigger problems
- For any $n_1 < n_2$, $f(n_1) \leq f(n_2)$
To make the math simpler, we'll allow fractional steps.
Asymptotic Analysis @ 5000 feet
Goal: Organize runtimes (growth functions) into different Complexity Classes.
Within a complexity class, runtimes "behave the same"
Big-Theta
The following are all saying the same thing
- $\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} = $ some non-zero constant.
- $f(n)$ and $g(n)$ have the same complexity.
- $f(n)$ and $g(n)$ are in the same complexity class.
- $f(n) \in \Theta(g(n))$
- $f(n)$ is bounded from above and below by $g(n)$
Big-Theta (As a Bound)
$f(n) \in \Theta(g(n))$ iff...
- $\exists c_{low}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \geq c_{low}\cdot g(n)$
- There is some $c_{low}$ that we can multiply $g(n)$ by so that $f(n)$ is always bigger than $c_{low}g(n)$ for values of $n$ above some $n_0$
- $\exists c_{high}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \leq c_{high}\cdot g(n)$
- There is some $c_{high}$ that we can multiply $g(n)$ by so that $f(n)$ is always smaller than $c_{high}g(n)$ for values of $n$ above some $n_0$
Proving Big-Theta
- Assume $f(n) \geq c_{low}g(n)$.
- Rewrite the above formula to find a $c_{low}$ for which it holds (for big enough n).
- Assume $f(n) \leq c_{high}g(n)$.
- Rewrite the above formula to find a $c_{high}$ for which it holds (for big enough n).
Shortcut: Find the dominant term being summed, and remove constants.
Common Runtimes
- Constant Time: $\Theta(1)$
- e.g., $T(n) = c$ (runtime is independent of $n$)
- Logarithmic Time: $\Theta(\log(n))$
- e.g., $T(n) = c\log(n)$ (for some constant $c$)
- Linear Time: $\Theta(n)$
- e.g., $T(n) = c_1n + c_0$ (for some constants $c_0, c_1$)
- Quadratic Time: $\Theta(n^2)$
- e.g., $T(n) = c_2n^2 + c_1n + c_0$
- Polynomial Time: $\Theta(n^k)$ (for some $k \in \mathbb Z^+$)
- e.g., $T(n) = c_kn^k + \ldots + c_1n + c_0$
- Exponential Time: $\Theta(c^n)$ (for some $c \geq 1$)
Other Bounds
$f(n) \in \Theta(g(n))$ iff...
- $\exists c_{low}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \geq c_{low}\cdot g(n)$
- There is some $c_{low}$ that we can multiply $g(n)$ by so that $f(n)$ is always bigger than $c_{low}g(n)$ for values of $n$ above some $n_0$
- $\exists c_{high}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \leq c_{high}\cdot g(n)$
- There is some $c_{high}$ that we can multiply $g(n)$ by so that $f(n)$ is always smaller than $c_{high}g(n)$ for values of $n$ above some $n_0$
Other Bounds
$f(n) \in O(g(n))$ iff...
- $\exists c_{low}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \geq c_{low}\cdot g(n)$
- There is some $c_{low}$ that we can multiply $g(n)$ by so that $f(n)$ is always bigger than $c_{low}g(n)$ for values of $n$ above some $n_0$
- $\exists c_{high}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \leq c_{high}\cdot g(n)$
- There is some $c_{high}$ that we can multiply $g(n)$ by so that $f(n)$ is always smaller than $c_{high}g(n)$ for values of $n$ above some $n_0$
Other Bounds
$f(n) \in \Omega(g(n))$ iff...
- $\exists c_{low}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \geq c_{low}\cdot g(n)$
- There is some $c_{low}$ that we can multiply $g(n)$ by so that $f(n)$ is always bigger than $c_{low}g(n)$ for values of $n$ above some $n_0$
- $\exists c_{high}, n_{0}$ s.t. $\forall n > n_{0}$, $f(n) \leq c_{high}\cdot g(n)$
- There is some $c_{high}$ that we can multiply $g(n)$ by so that $f(n)$ is always smaller than $c_{high}g(n)$ for values of $n$ above some $n_0$
Other Bounds
- Big-O: "Worst Case" bound
- The set of all functions in the same or a smaller complexity class (same or faster runtime).
- Big-Ω: "Best Case" bound
- The set of all functions in the same or a bigger complexity class (same or slower runtime).
- Big-ϴ: "Tight" bound
- The set of all functions in the same complexity class (same runtime).
- "Tight Worst Case"
- $n^2 \in O(n^3)$ is true, but you can do better.
$\Theta(g(n)) = O(g(n)) \cap \Omega(g(n))$
$\Theta$ is the same as ($O$ and $\Omega$)
Analyzing Code
The growth function for a block of code...
- One Line of Code
- Sum the growth functions of every method the line invokes.
- Lines of Sequential Code
- Sum up the growth function of each line of code.
- Loops
- Use a summation ($\sum$) over the body of the loop.
- (Shorthand: $k$ loops with a $O(f(n))$ body = $O(k\cdot f(n))$
Sequences
The Seq ADT
- apply(idx: Int): A
- Get the element (of type A) at position idx.
- iterator: Iterator[A]
- Get access to view all elements in the seq, in order, once.
- length: Int
- Count the number of elements in the seq.
The mutable.Seq ADT
- apply(idx: Int): A
- Get the element (of type A) at position idx.
- iterator: Iterator[A]
- Get access to
- view
- length: Int
- Count the number of elements in the seq.
- insert(idx: Int, elem: A): Unit
- Insert an element at position idx with value elem.
- remove(idx: Int): A
- Remove the element at position idx and return the removed value.
Sequence Implementations
- Linked List
- $O(1)$ mutations by reference or head/tail, $O(n)$ otherwise
- Array
- $O(1)$ access/update, $O(n)$ insert/remove
- ArrayBuffer
- $O(1)$ access/update, $O(n)$ insert/remove
- $O(1)$ amortized append
Amortized $O(1)$
- Bounds for one call:
- Amortized says nothing.
- Bounds for $n$ calls:
- Guaranteed always $< n\cdot O(1)$.
Expected $O(1)$
No guarantees at all!
Guarantees
- Tight $\Theta(f(n))$
- The cost of one call will always be a constant factor from $f(n)$.
- Worst Case $O(f(n))$
- The cost of one call will never be worse than a constant factor from $f(n)$.
- Amortized Worst Case $O(f(n))$
- The cost of n calls will never be worse than a constant factor from $n \cdot f(n)$.
- Expected Worst Case $O(f(n))$
- "Usually" not worse than a constant factor from $f(n)$, but no promises.
Sequences
| Operation | Array | ArrayBuffer | LinkedList by Index | LinkedList by Ref |
|---|---|---|---|---|
| apply | $O(1)$ | $O(1)$ | $O(n)$ or $O(i)$ | $O(1)$ |
| update | $O(1)$ | $O(1)$ | $O(n)$ or $O(i)$ | $O(1)$ |
| insert | $O(n)$ | $O(n)$ or Amortized $O(n-i)$ |
$O(n)$ or $O(i)$ | $O(1)$ |
| remove | $O(n)$ | $O(n)$ or $O(n-i)$ | $O(n)$ or $O(i)$ | $O(1)$ |
| append | $O(n)$ | $O(n)$ or Amortized $O(1)$ | $O(n)$ or $O(i)$ | $O(1)$ |
Recursion
Fibonacci
What's the complexity? (in terms of n)
def fibb(n: Int): Long =
if(n < 2){ 1 }
else { fibb(n-1) + fibb(n-2) }
Fibonacci
$$T(n) = \begin{cases} \Theta(1) & \textbf{if } n < 2\\ T(n-1) + T(n-2) + \Theta(1) & \textbf{otherwise} \end{cases}$$Test Hypothesis: $T(n) \in O(2^n)$
Merge Sort
def merge[A: Ordering](left: Seq[A], right: Seq[A]): Seq[A] = {
val output = ArrayBuffer[A]()
val leftItems = left.iterator.buffered
val rightItems = right.iterator.buffered
while(leftItems.hasNext || rightItems.hasNext) {
if(!left.hasNext) { output.append(right.next) }
else if(!right.hasNext) { output.append(left.next) }
else if(Ordering[A].lt( left.head, right.head ))
{ output.append(left.next) }
else { output.append(right.next) }
}
output.toSeq
}
Merge Sort
Each time though loop advances either left or right.
Total Runtime: $\Theta(|\texttt{left}| + |\texttt{right}|)$
Merge Sort
Observation: Merging two sorted arrays can be done in $O(n)$.
Idea: Split the input in half, sort each half, and merge.
Merge Sort
def sort[A: Ordering](data: Seq[A]): Seq[A] =
{
if(data.length <= 1) { return data }
else {
val (left, right) = data.splitAt(data.length / 2)
return merge(
sort(left),
sort(right)
)
}
}
Merge Sort
- Divide: Split the sequence in half
- $D(n) = \Theta(n)$ (can do in $\Theta(1)$)
- Conquer: Sort left and right halves
- $a = 2$, $b = 2$, $c = 1$
- Combine: Merge halves together
- $C(n) = \Theta(n)$
Merge Sort
$$T(n) = \begin{cases} \Theta(1) & \textbf{if } n \leq 1 \\ 2\cdot T(\frac{n}{2}) + \Theta(1) + \Theta(n) & \textbf{otherwise} \end{cases}$$How can we find a closed-form hypothesis?
Idea: Draw out the cost of each level of recursion.
Merge Sort: Recursion Tree
$$T(n) = \begin{cases} \Theta(1) & \textbf{if } n \leq 1 \\ 2\cdot T(\frac{n}{2}) + \Theta(1) + \Theta(n) & \textbf{otherwise} \end{cases}$$Each node of the tree shows $D(n) + C(n)$
Hypothesis: $n \cdot \log(n)$
Merge Sort: Proof By Induction
Now use induction to prove that there is a $c, n_0$
such that $T(n) \leq c \cdot n\log(n)$ for any $n > n_0$
Merge Sort: Proof By Induction
Base Case: $T(1) \leq c \cdot 1$
$$c_0 \leq c$$
True for any $c > c_0$
Merge Sort: Proof By Induction
Assume: $T(\frac{n}{2}) \leq c \frac{n}{2} \log\left(\frac{n}{2}\right)$
Show: $T(n) \leq c n \log\left(n\right)$
$$2\cdot T(\frac{n}{2}) + c_1 + c_2 n \leq c n \log(n)$$
By the assumption and transitivity, showing the following inequality suffices:
$$2 c \frac{n}{2} \log\left(\frac{n}{2}\right) + c_1 + c_2 n \leq c n \log(n)$$
$$c n \log(n) - c n \log(2) + c_1 + c_2 n \leq c n \log(n)$$
$$c_1 + c_2 n \leq c n \log(2)$$
$$\frac{c_1}{n \log(2)} + \frac{c_2}{\log(2)} \leq c$$
True for any $n_0 \geq \frac{c_1}{\log(2)}$ and $c > \frac{c_2}{\log(2)}+1$
Stacks and Queues
Stacks vs Queues
- Push
- Put a new object on top of the stack
- Pop
- Remove the object on top of the stack
- Top
- Peek at what's on top of the stack
- Enqueue
- Put a new object at the end of the queue
- Dequeue
- Remove the next object in the queue
- Head
- Peek at the next object in the queue
Queues vs Stacks
- Queue
- First in, First out (FIFO)
- Stack
- Last in, First Out (LIFO / FILO)
Graphs
Graphs
A graph is a pair $(V, E)$ where
- $V$ is a set of vertices
- $E$ is a set of vertex pairs called edges
- edges and vertices may also store data (labels)
Edge Types
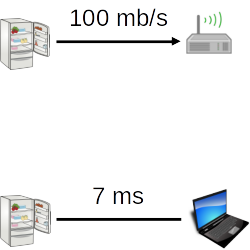
- Directed Edge (e.g., transmit bandwidth)
- Ordered pair of vertices $(u, v)$
- origin ($u$) → destination ($v$)
- Undirected edge (e.g., round-trip latency)
- Unordered pair of vertices $(u, v)$
- Directed Graph
- All edges are directed
- Undirected Graph
- All edges are undirected
Terminology
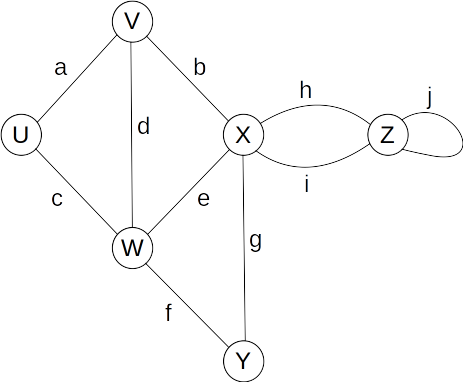
- Endpoints (end-vertices) of an edge
- U, V are the endpoints of a
- Edges incident on a vertex
- a, b, d are incident on V
- Adjacent Vertices
- U, V are adjacent
- Degree of a vertex (# of incident edges)
- X has degree 5
- Parallel Edges
- h, i are parallel
- Self-Loop
- j is a self-loop
- Simple Graph
- A graph without parallel edges or self-loops
Notation
- $n$
- The number of vertices
- $m$
- The number of edges
- $deg(v)$
- The degree of vertex $v$
Graph Properties
$$\sum_{v} deg(v) = 2m$$Proof: Each edge is counted twice
Graph Properties
In a directed graph with no self-loops and no parallel edges:
$$m \leq n(n-1)$$
- No parallel edges: each pair connected at most once
- No self loops: pick each vertex once
$n$ choices for the first vertex
$(n-1)$ choices for the second vertex
$$m \leq n(n-1)$$
A (Directed) Graph ADT
- Two type parameters (Graph[V, E])
- V: The vertex label type
- E: The edge label type
- Vertices
- ... are elements (like Linked List Nodes)
- ... store a value of type V
- Edges
- ... are elements
- ... store a value of type E
A (Directed) Graph ADT
trait Graph[V, E] {
def vertices: Iterator[Vertex]
def edges: Iterator[Edge]
def addVertex(label: V): Vertex
def addEdge(orig: Vertex, dest: Vertex, label: E): Edge
def removeVertex(vertex: Vertex): Unit
def removeEdge(edge: Edge): Unit
}
A (Directed) Graph ADT
trait Vertex[V, E] {
def outEdges: Seq[Edge]
def inEdges: Seq[Edge]
def incidentEdges: Iterator[Edge] = outEdges ++ inEdges
def edgeTo(v: Vertex): Boolean
def label: V
}
trait Edge[V, E] {
def origin: Vertex
def destination: Vertex
def label: E
}
Edge List
Edge List Summary
- addEdge, addVertex: $O(1)$
- removeEdge: $O(1)$
- removeVertex: $O(m)$
- vertex.incidentEdges: $O(m)$
- vertex.edgeTo: $O(m)$
- Space Used: $O(n) + O(m)$
Idea: Store the in/out edges for each vertex.
Attempt 3: Adjacency List
class DirectedGraphV3[V, E] extends Graph[V, E] {
/* ... */
class Vertex(label: V) = {
var node: DoublyLinkedList[Vertex].Node = null
val inEdges = DoublyLinkedList[Edge]()
val outEdges = DoublyLinkedList[Edge]()
/* ... */
}
class Edge(orig: Vertex, dest: Vertex, label: E) = {
var node: DoublyLinkedList[Edge].Node = null
var origNode: DoublyLinkedList[Edge].Node = null
var destNode: DoublyLinkedList[Edge].Node = null
/* ... */
}
/* ... */
}Adjacency List Summary
- addEdge, addVertex: $O(1)$
- removeEdge: $O(1)$
- vertex.incidentEdges: $O(deg(vertex))$
- removeVertex: $O(deg(vertex))$
- vertex.edgeTo: $O(deg(vertex))$
- Space Used: $O(n) + O(m)$
A few more definitions...
- A subgraph $S$ of a graph $G$ is a graph where...
- $S$'s vertices are a subset of $G$'s vertices
- $S$'s edges are a subset of $G$'s edges
- A spanning subgraph of $G$...
- Is a subgraph of $G$
- Contains all of $G$'s vertices.
A few more definitions...
- A graph is connected...
- If there is a path between every pair of vertices
- A connected component of $G$...
- Is a maximal connected subgraph of $G$
- "maximal" means you can't add any new vertex without breaking the property
- Any subset of $G$'s edges that connects the subgraph is fine.
A few more definitions...
- A free tree is an undirected graph $T$ such that:
- There is exactly one simple path between any two nodes
- T is connected
- T has no cycles
- A rooted tree is a directed graph $T$ such that:
- One vertex of $T$ is the root
- There is exactly one simple path from the root to every other vertex in the graph.
- A (free/rooted) forest is a graph $F$ such that
- Every connected component is a tree.
A few more definitions...
- A spanning tree of a connected graph...
- Is a spanning subgraph that is a tree.
- Is not unique unless the graph is a tree.
Depth-First Search
Summing up...
| Mark Vertices UNVISITED | $O(|V|)$ |
| Mark Edges UNVISITED | $O(|E|)$ |
| DFS Vertex Loop | $O(|V|)$ |
| All Calls to DFSOne | $O(|E|)$ |
| $O(|V| + |E|)$ |
Depth-First Search
Summing up...
| Mark Vertices UNVISITED | $O(|V|)$ |
| Mark Edges UNVISITED | $O(|E|)$ |
| Add each vertex to the work queue | $O(|V|)$ |
| Process each vertex | $O(|E|)$ |
| $O(|V| + |E|)$ |
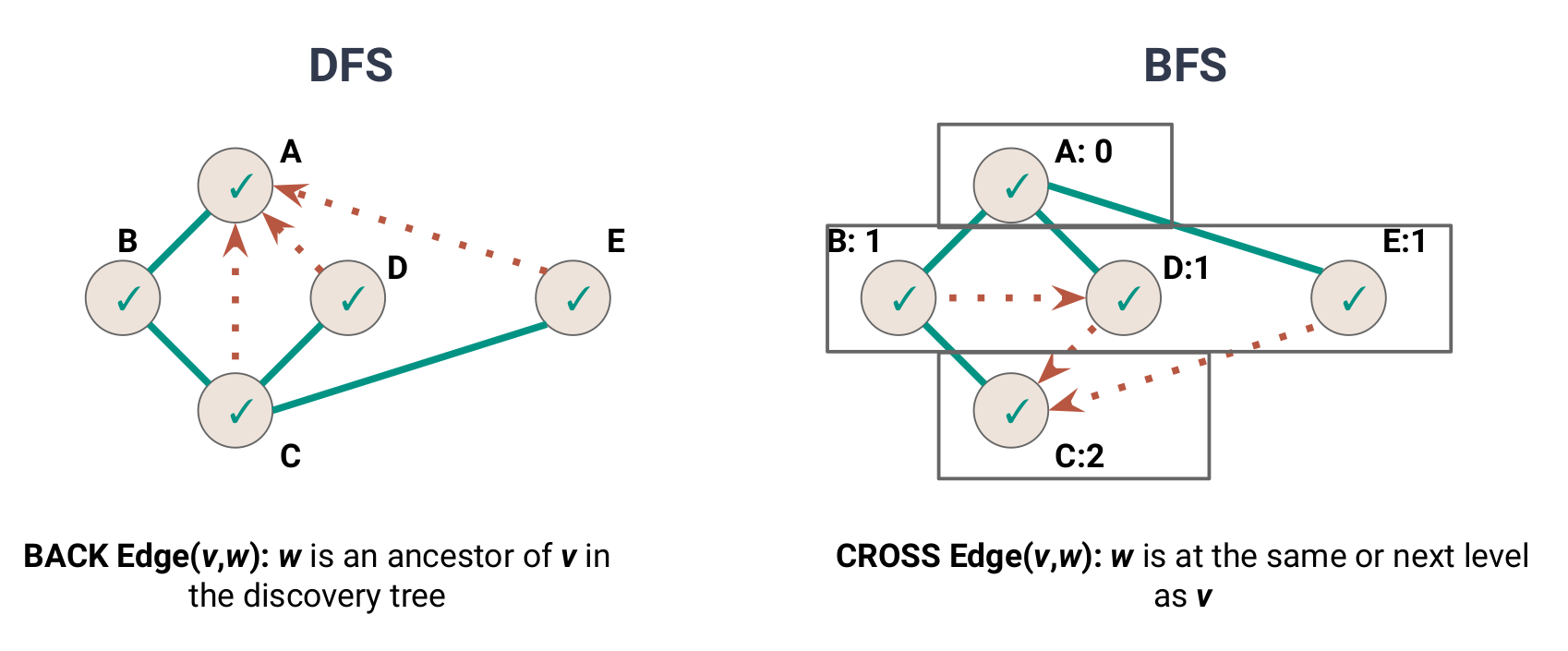
| Application | DFS | BFS |
|---|---|---|
| Spanning Trees | ✔ | ✔ |
| Connected Components | ✔ | ✔ |
| Paths/Connectivity | ✔ | ✔ |
| Cycles | ✔ | ✔ |
| Shortest Paths | ✔ | |
| Articulation Points | ✔ |
DFS vs BFS